Matura matematyka - arkusze maturalne (podstawowy 2012)
| WYBIERZ ILOŚĆ PYTAŃ: | |
KAŻDY TEST ZAWIERA LOSOWY UKŁAD PYTAŃ I ODPOWIEDZI
Jeżeli chcesz rozwiązywać test w całości to zaznacz wszystkie dostępne typy zadań oraz wybierz maksymalną ilość pytań. Jeżeli chcesz rozwiązać szybki test to pozostaw domyślne ustawienia lub zmniejsz jeszcze ilość pytań. Możesz np. rozwiązywać tylko 'zadania zamknięte' i 'wybór z listy', jeżeli nie chcesz pisać własnych odpowiedzi. Wybór należy do Ciebie.
WYBÓR Z LISTY - pytania, w których należy wybrać odpowiedź z listy możliwych odpowiedzi.
UZUPEŁNIANIE LUK - pytania, w których należy samodzielnie uzupełniać luki w tekście.
KRÓTKA ODPOWIEDŹ PISEMNA - pytania, w których należy samodzielnie napisać krótką odpowiedź.
WYRACOWANIA - pytania, w których należy samodzielnie napisać dłuższą odpowiedź na zadany temat.
KRÓTKA INSTRUKCJA OBSŁUGI:
- Wybierz testy, z których chcesz losować zadania. Domyślnie zaznaczony jest test, których został wybrany na poprzedniej liście testów. Jeżeli chcesz losować zadania, z kilku różnych testów, kliknij na 'KLIKNIJ ABY WYBRAĆ ZAKRES PYTAŃ' i zaznacz testy. Wszystkie wybrane testy będą uwzględnione w losowaniu zadań.
- Wybierz typy zadań jakie mają być dostępne w teście.
- Wybierz maksymalną liczbę pytań. Jeżeli nie zaznaczono wszystkich typów zadań, to liczba pytań w teście może być mniejsza niż wybrano.
- Kliknij na 'ROZWIĄŻ TEST.
Matura matematyka - arkusze maturalne (podstawowy 2012) - przykładowe pytania:
Liczba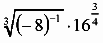 jest równa ........ Iloczyn
jest równa ........ Iloczyn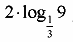 jest równy ........ Liczby x1, x2 są różnymi rozwiązaniami równania 2x2+3x-7=0 Suma x1+x2 jest równa: ........ Funkcja liniowa f jest określona wzorem f (x)=ax+6, gdzie a> 0. Wówczas spełniony jest warunek ........ Liczba tg30°-sin30° jest równa ........ W trójkącie równoramiennym ABC dane są |AC|=|BC|=5 oraz wysokość |CD|=2. Podstawa AB tego trójkąta ma długość ........ Odcinki AB i CD są równoległe i |AB|=5, |AC|=2, |CD|=7 (zobacz rysunek). Długość odcinka AE jest równa ........ Punkty A, B, C, D dzielą okrąg na 4 równe łuki. Miara zaznaczonego na rysunku kąta wpisanego ACD jest równa ........
jest równy ........ Liczby x1, x2 są różnymi rozwiązaniami równania 2x2+3x-7=0 Suma x1+x2 jest równa: ........ Funkcja liniowa f jest określona wzorem f (x)=ax+6, gdzie a> 0. Wówczas spełniony jest warunek ........ Liczba tg30°-sin30° jest równa ........ W trójkącie równoramiennym ABC dane są |AC|=|BC|=5 oraz wysokość |CD|=2. Podstawa AB tego trójkąta ma długość ........ Odcinki AB i CD są równoległe i |AB|=5, |AC|=2, |CD|=7 (zobacz rysunek). Długość odcinka AE jest równa ........ Punkty A, B, C, D dzielą okrąg na 4 równe łuki. Miara zaznaczonego na rysunku kąta wpisanego ACD jest równa ........ WYBRANE WYMAGANIA EGZAMINACYJNE Z MATEMATYKI:
|
POZIOM PODSTAWOWY |
POZIOM ROZSZERZONY |
|
|
|
1) liczby rzeczywiste |
jak na poziomie podstawowym oraz: a) stosuje twierdzenie o rozkładzie liczby naturalnej na czynniki pierwsze; wyznacza największy wspólny dzielnik i najmniejszą wspólną wielokrotność pary liczb naturalnych, b) stosuje wzór na logarytm potęgi i wzór na zamianę podstawy logarytmu, |
|
|
|
| 2) wyrażenia algebraiczne: a) posługuje się wzorami skróconego mnożenia b) rozkłada wielomian na czynniki stosując wzory skróconego mnożenia, grupowanie wyrazów, wyłączanie wspólnego czynnika poza nawias, c) dodaje, odejmuje i mnoży wielomiany, d) wyznacza dziedzinę prostego wyrażenia wymiernego z jedną zmienną, w którym w mianowniku występują tylko wyrażenia dające się sprowadzić do iloczynu wielomianów liniowych i kwadratowych za pomocą przekształceń opisanych w punkcie b), e) oblicza wartość liczbową wyrażenia wymiernego dla danej wartości zmiennej, f) dodaje, odejmuje, mnoży i dzieli wyrażenia wymierne; skraca i rozszerza wyrażenia wymierne, |
jak na poziomie podstawowym oraz: a) posługuje się wzorem (a -1)(a + ...+ an-1) = an - 1, b) wykonuje dzielenie wielomianu przez dwumian x-a; stosuje twierdzenie o reszcie z dzielenia wielomianu przez dwumian x-a, c) stosuje twierdzenie o pierwiastkach wymiernych wielomianu o współczynnikach całkowitych, |
|
|
|
3) równania i nierówności: |
jak na poziomie podstawowym oraz: |
|
|
|
| 4) funkcje: a) określa funkcję za pomocą wzoru, tabeli, wykresu, opisu słownego, b) odczytuje z wykresu funkcji: dziedzinę i zbiór wartości, miejsca zerowe, maksymalne przedziały, w których funkcja rośnie, maleje, ma stały znak, c) sporządza wykres funkcji spełniającej podane warunki, d) potrafi na podstawie wykresu funkcji y = f (x) naszkicować wykresy funkcji y = f (x + a), y = f (x) + a, y = -f (x), y =f (-x ) e) sporządza wykresy funkcji liniowych, f) wyznacza wzór funkcji liniowej, g) wykorzystuje interpretację współczynników we wzorze funkcji liniowej, h) sporządza wykresy funkcji kwadratowych, i) wyznacza wzór funkcji kwadratowej, j) wyznacza miejsca zerowe funkcji kwadratowej, k) wyznacza wartość najmniejszą i wartość największą funkcji kwadratowej w przedziale domkniętym, l) rozwiązuje zadania (również umieszczone w kontekście praktycznym), prowadzące do badania funkcji kwadratowej, m) sporządza wykres, odczytuje własności i rozwiązuje zadania umieszczone w kontekście praktycznym związane z proporcjonalnością odwrotną, n) sporządza wykresy funkcji wykładniczych dla różnych podstaw i rozwiązuje zadania umieszczone w kontekście praktycznym, |
jak na poziomie podstawowym oraz: mając dany wykres funkcji y = f (x) potrafi naszkicować: a) wykres funkcji y = |f (x)|, b) wykresy funkcji y = c • f (x), y = f (c • x), gdzie f jest funkcją trygonometryczną, c) wykres będący efektem wykonania kilku operacji, na przykład y = |f (x + 2) - 3|, d) wykresy funkcji logarytmicznych dla różnych podstaw, e) rozwiązuje zadania (również umieszczone w kontekście praktycznym) z wykorzystaniem takich funkcji, |
WSZYSTKIE WYMAGANIA SĄ ZAWARTE W INFORMATORZE
Korzystanie z serwisu oznacza akceptację Regulaminu i Polityki Prywatności
(Ostatnie zmiany: 24.05.2018r)